피타고라스의 수와 새로운 공식 소개
피타고라스의 정리는 직각삼각형에서 빗변의 제곱이 다른 두 변의 제곱의 합과 같다는 내용을 말합니다.
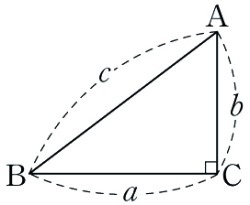
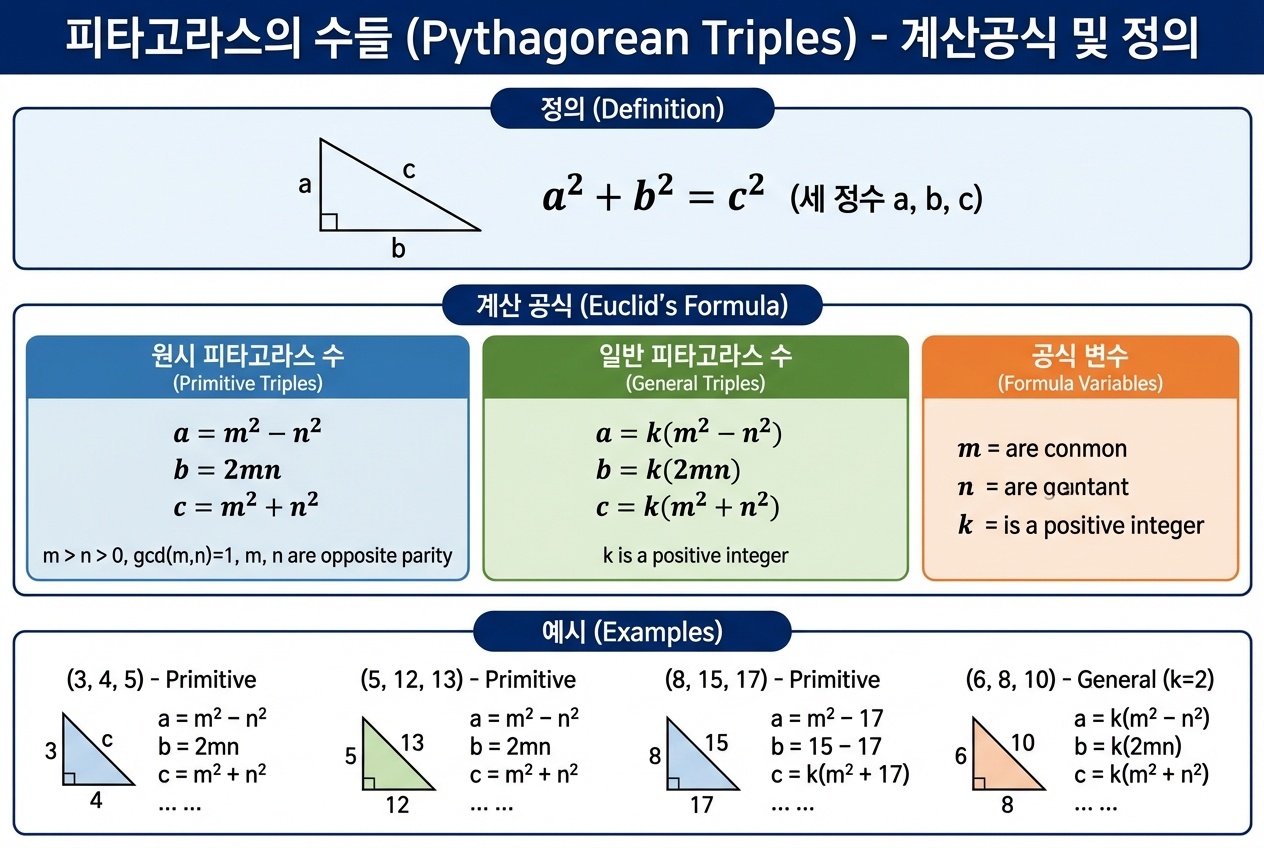
이 정리에서 도출되는 피타고라스의 수는 (a, b, c)처럼 세 개의 정수로 이루어진 집합이며, a² + b² = c²를 만족합니다. 대표적인 예로 (3, 4, 5), (5, 12, 13), (7, 24, 25) 등이 있습니다.

피타고라스의 수를 구하는 기본적인 방법으로는 유클리드 공식이 오래전부터 널리 사용되어 왔습니다.
유클리드 공식
유클리드 공식은 다음과 같습니다.
a = m^2 - n^2,
b = 2mn,
c = m^2 + n^2여기서 m과 n은 정수이며, m > n의 조건을 만족해야 합니다.
단순하고 강력하지만, 모든 피타고라스의 수를 정리해 나열하거나 계산을 반복할 때는 불편함을 느낄 수 있습니다.
피타고라스의 수들
| 피타고라스 수 | |||
| (3, 4, 5) | (5, 12, 13) | (6, 8, 10) | (7, 24, 25) |
| (8, 15, 17) | (9, 12, 15) | (9, 40, 41) | (10, 24, 26) |
| (11, 60, 61) | (12, 16, 20) | (12, 35, 37) | (13, 84, 85) |
| (14, 48, 50) | (15, 20, 25) | (15, 36, 39) | (15, 112, 113) |
| (16, 30, 34) | (16, 63, 65) | (17, 144, 145) | (18, 24, 30) |
| (18, 80, 82) | (19, 180, 181) | (20, 21, 29) | (20, 48, 52) |
| (20, 99, 101) | (21, 28, 35) | (21, 72, 75) | (21, 220, 221) |
| (22, 120, 122) | (23, 264, 265) | (24, 32, 40) | (24, 45, 51) |
| (24, 70, 74) | (24, 143, 145) | (25, 60, 65) | (25, 312, 313) |
| (26, 168, 170) | (27, 36, 45) | (27, 120, 123) | (27, 364, 365) |
| (28, 45, 53) | (28, 96, 100) | (28, 195, 197) | (29, 420, 421) |
| (30, 40, 50) | (30, 72, 78) | (30, 224, 226) | (31, 480, 481) |
| (32, 60, 68) | (32, 126, 130) | (32, 255, 257) | (33, 44, 55) |
| (33, 56, 65) | (33, 180, 183) | (33, 544, 545) | (34, 288, 290) |
| (35, 84, 91) | (35, 120, 125) | (36, 48, 60) | (36, 77, 85) |
| (36, 105, 111) | (36, 160, 164) | (36, 323, 325) | (38, 360, 362) |
| (39, 52, 65) | (39, 80, 89) | (39, 252, 255) | (40, 42, 58) |
| (40, 75, 85) | (40, 96, 104) | (40, 198, 202) | (40, 399, 401) |
| (42, 56, 70) | (42, 144, 150) | (42, 440, 442) | (44, 117, 125) |
| (44, 240, 244) | (44, 483, 485) | (45, 60, 75) | (45, 108, 117) |
| (45, 200, 205) | (45, 336, 339) | (46, 528, 530) | (48, 55, 73) |
| (48, 64, 80) | (48, 90, 102) | (48, 140, 148) | (48, 189, 195) |
| (48, 286, 290) | (48, 575, 577) | (51, 68, 85) | (51, 140, 149) |
| (52, 165, 173) | (52, 336, 340) | (54, 72, 90) | (54, 240, 246) |
| (55, 132, 143) | (55, 300, 305) | (56, 90, 106) | (56, 105, 119) |
| (56, 192, 200) | (56, 390, 394) | (57, 76, 95) | (57, 176, 185) |
| (57, 540, 543) | (60, 63, 87) | (60, 80, 100) | (60, 91, 109) |
| (60, 144, 156) | (60, 175, 185) | (60, 221, 229) | (60, 297, 303) |
새로운 공식의 도입
기존의 유클리드 공식에서 느껴지는 불편함을 줄이기 위해, 원문에서는 새로운 형태로 정리한 식을 제안했습니다.
유클리드 공식에서 m = n + k라고 가정하고 정리하면, 아래처럼 전개할 수 있습니다.
[ a = (n + k)^2 - n^2, \quad b = 2(n + k)n, \quad c = (n + k)^2 + n^2 ]이를 다시 정리하면 다음과 같습니다.
[ a = n^2 + 2nk + k^2 - n^2 = 2nk + k^2 ] [ b = 2n(n + k) = 2n^2 + 2nk ] [ c = n^2 + 2nk + k^2 + n^2 = 2n^2 + 2nk + k^2 ]여기서 k를 m으로 바꾸어 표기하면,
[ a = 2nm + m^2 ] [ b = 2n^2 + 2mn ] [ c = 2n^2 + 2nm + m^2 ]원문 기준으로 이 식은 m과 n이 정수라는 조건을 유지하면서, 계산 시 더 직관적으로 쓸 수 있는 형태로 정리된 공식입니다.
사용 예시
새롭게 정리한 공식을 이용해 예시를 들면, m = 1일 때 다음과 같은 결과를 얻습니다.
[ a = 2n \cdot 1 + 1^2 = 2n + 1 ] [ b = 2n^2 + 2n \cdot 1 = 2n^2 + 2n ] [ c = 2n^2 + 2n \cdot 1 + 1^2 = 2n^2 + 2n + 1 ]이처럼 n과 m의 값에 따라 여러 가지 피타고라스의 수를 간단히 도출할 수 있습니다.
결론적으로 피타고라스의 수는 무한하게 존재하며, 이를 구하는 방법도 여러 형태로 정리할 수 있습니다.
정리하면, 유클리드 공식은 기본적인 방법으로 많이 사용되어 왔고, 원문에서 제안한 정리식은 더 직관적이고 편리하게 활용될 수 있습니다.
이 공식을 이용하면 다양한 피타고라스의 수를 쉽게 찾아낼 수 있으니, 직접 값을 대입해보며 여러 조합을 만들어 보는 것도 좋습니다.
FAQ
Q. 피타고라스의 수는 어떤 조건을 만족하나요?
A. (a, b, c) 세 정수가 a² + b² = c²를 만족하는 경우를 말합니다.
Q. 유클리드 공식의 기본 형태는 무엇인가요?
A. 정수 m, n(m > n)에 대해 a = m^2 - n^2, b = 2mn, c = m^2 + n^2입니다.
Q. 글에서 말한 “새로운 공식”은 어떻게 나온 건가요?
A. 유클리드 공식에서 m = n + k로 두고 전개한 뒤 정리해 얻은 형태입니다.
Q. m = 1로 두면 어떤 식이 되나요?
A. a = 2n + 1, b = 2n^2 + 2n, c = 2n^2 + 2n + 1로 정리됩니다.
Q. 피타고라스의 수가 무한히 존재한다는 말은 어떤 의미인가요?
A. 원문처럼 m과 n을 정수로 두고 여러 값을 대입하면 (a, b, c)가 계속 생성되기 때문에, 가능한 조합이 끝없이 이어집니다.
'3D 2D 디자인 > Semens UG NX' 카테고리의 다른 글
| UG NX 매크로 사용법 및 설정 - 기록 및 재생 실행방법 (0) | 2025.03.19 |
|---|---|
| Siemens NX X 클라우드 기반 구독형 CAD 라이센스 차이점 (0) | 2025.02.28 |
| 3D CAD 그래픽카드 라데온 VS 쿼드로 성능비교 왜 좋을까? (1) | 2025.01.02 |



