피타고라스의 수와 새롭게 정리한 계산식
직각삼각형에서 가장 유명한 관계식이 바로 피타고라스의 정리입니다.
두 직각변을 a, b, 빗변을 c라 두면 a² + b² = c²가 성립하죠. 이 등식이 “정수”에서 딱 떨어지게 맞아떨어지는 경우를 모아둔 것이 피타고라스의 수(피타고라스 삼쌍)입니다.
대표 예시는 (3, 4, 5), (5, 12, 13), (7, 24, 25)처럼 익숙한 조합이고, 이들은 모두 a² + b² = c²를 만족합니다. 여기서 알아두면 좋은 구분이 하나 더 있습니다.
원시(Primitive) 삼쌍과 배수 삼쌍
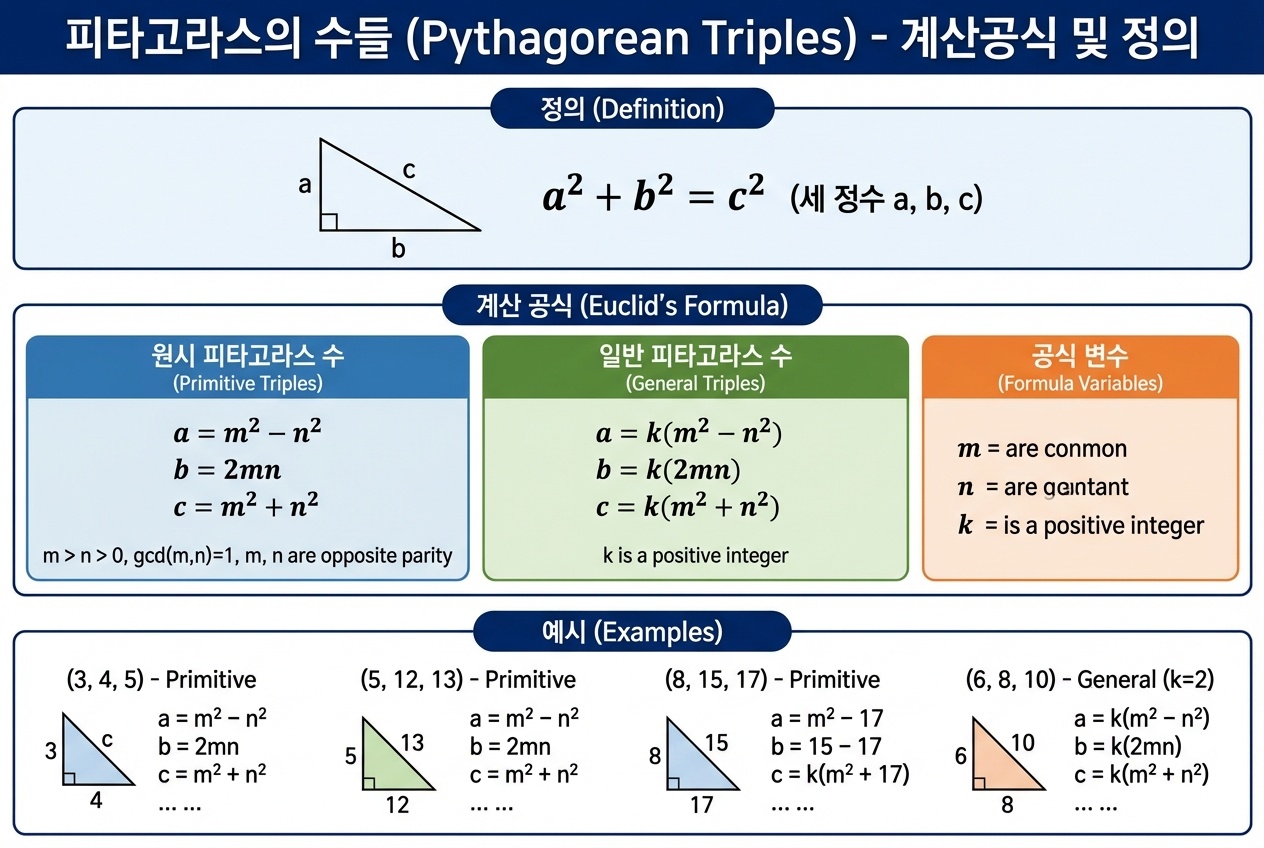
(3, 4, 5)는 세 수의 최대공약수가 1이라서 원시 피타고라스 삼쌍입니다. 반면 (6, 8, 10)은 (3, 4, 5)의 2배라서 배수 삼쌍으로 분류합니다. 검색을 해도 예시가 섞여 나오는 일이 많아서, 글을 읽는 입장에선 이 구분을 알고 보면 훨씬 정리가 잘 됩니다.
피타고라스의 수들 - 계산공식 및 정의
피타고라스의 수와 새로운 공식 소개피타고라스의 정리는 수학의 기초적인 원리 중 하나로, 직각삼각형의 빗변의 제곱이 다른 두 변의 제곱의 합과 같다는 것을 말합니다.그리고 이 정리에서
jab-guyver.co.kr
유클리드 공식: 가장 표준적인 생성식
피타고라스의 수를 “한 번에” 만들어내는 대표 공식이 유클리드 공식입니다. 정수 m, n(m > n)를 두고
a = m² − n², b = 2mn, c = m² + n²
이 조합은 항상 피타고라스의 정리를 만족합니다. 추가로 원시 삼쌍만 뽑고 싶다면, 보통 아래 조건을 같이 봅니다.
- gcd(m, n) = 1 (서로소)
- m과 n 중 하나는 짝수, 하나는 홀수 (둘 다 홀수면 세 수가 전부 짝수가 되는 쪽으로 쏠림)
이 조건을 같이 잡으면 “중복 없이” 깔끔하게 원시 삼쌍을 뽑아낼 수 있습니다.
피타고라스의 수들 (일부 예시)
| 피타고라스 수 | |||
| (3, 4, 5) | (5, 12, 13) | (6, 8, 10) | (7, 24, 25) |
| (8, 15, 17) | (9, 12, 15) | (9, 40, 41) | (10, 24, 26) |
| (11, 60, 61) | (12, 16, 20) | (12, 35, 37) | (13, 84, 85) |
| (14, 48, 50) | (15, 20, 25) | (15, 36, 39) | (15, 112, 113) |
| (16, 30, 34) | (16, 63, 65) | (17, 144, 145) | (18, 24, 30) |
| (18, 80, 82) | (19, 180, 181) | (20, 21, 29) | (20, 48, 52) |
| (20, 99, 101) | (21, 28, 35) | (21, 72, 75) | (21, 220, 221) |
| (22, 120, 122) | (23, 264, 265) | (24, 32, 40) | (24, 45, 51) |
| (24, 70, 74) | (24, 143, 145) | (25, 60, 65) | (25, 312, 313) |
| (26, 168, 170) | (27, 36, 45) | (27, 120, 123) | (27, 364, 365) |
| (28, 45, 53) | (28, 96, 100) | (28, 195, 197) | (29, 420, 421) |
| (30, 40, 50) | (30, 72, 78) | (30, 224, 226) | (31, 480, 481) |
| (32, 60, 68) | (32, 126, 130) | (32, 255, 257) | (33, 44, 55) |
| (33, 56, 65) | (33, 180, 183) | (33, 544, 545) | (34, 288, 290) |
| (35, 84, 91) | (35, 120, 125) | (36, 48, 60) | (36, 77, 85) |
| (36, 105, 111) | (36, 160, 164) | (36, 323, 325) | (38, 360, 362) |
| (39, 52, 65) | (39, 80, 89) | (39, 252, 255) | (40, 42, 58) |
| (40, 75, 85) | (40, 96, 104) | (40, 198, 202) | (40, 399, 401) |
| (42, 56, 70) | (42, 144, 150) | (42, 440, 442) | (44, 117, 125) |
| (44, 240, 244) | (44, 483, 485) | (45, 60, 75) | (45, 108, 117) |
| (45, 200, 205) | (45, 336, 339) | (46, 528, 530) | (48, 55, 73) |
| (48, 64, 80) | (48, 90, 102) | (48, 140, 148) | (48, 189, 195) |
| (48, 286, 290) | (48, 575, 577) | (51, 68, 85) | (51, 140, 149) |
| (52, 165, 173) | (52, 336, 340) | (54, 72, 90) | (54, 240, 246) |
| (55, 132, 143) | (55, 300, 305) | (56, 90, 106) | (56, 105, 119) |
| (56, 192, 200) | (56, 390, 394) | (57, 76, 95) | (57, 176, 185) |
| (57, 540, 543) | (60, 63, 87) | (60, 80, 100) | (60, 91, 109) |
| (60, 144, 156) | (60, 175, 185) | (60, 221, 229) | (60, 297, 303) |
“새로운 공식”처럼 보이는 재정리: 변수만 바꿔서 더 빨리 쓰는 방식
유클리드 공식이 강력하긴 한데, 실제로 계산할 땐 “m과 n의 차이”를 먼저 떠올리는 편이 더 자연스러운 경우가 있습니다.
그래서 m = n + k처럼 두 값의 간격을 따로 두고 다시 풀어 쓰면, 식이 좀 더 손에 익는 형태로 바뀝니다.
유도식(원문 코드 그대로)
유클리드 공식에서 m = n + k라고 두면 다음과 같이 쓸 수 있습니다.
[ a = (n + k)^2 - n^2, \quad b = 2(n + k)n, \quad c = (n + k)^2 + n^2 ]정리하면,
[ a = n^2 + 2nk + k^2 - n^2 = 2nk + k^2 ] [ b = 2n(n + k) = 2n^2 + 2nk ] [ c = n^2 + 2nk + k^2 + n^2 = 2n^2 + 2nk + k^2 ]여기서 k를 m으로 바꿔 적으면(표기만 바꾼 형태),
[ a = 2nm + m^2 ] [ b = 2n^2 + 2mn ] [ c = 2n^2 + 2nm + m^2 ]핵심은 “새로운 정리”라기보다 유클리드 공식을 한 번 더 다듬어 계산 흐름을 단순하게 만든 재표현에 가깝다는 점입니다.
실제로 써보면 n을 잡고 m을 조금씩 바꾸는 방식이 손에 붙는 분들이 꽤 많습니다.
사용 예시(원문 코드 그대로)
예를 들어 m = 1로 두면,
[ a = 2n \cdot 1 + 1^2 = 2n + 1 ] [ b = 2n^2 + 2n \cdot 1 = 2n^2 + 2n ] [ c = 2n^2 + 2n \cdot 1 + 1^2 = 2n^2 + 2n + 1 ]이 형태는 a가 항상 홀수로 나오고, b는 n이 커질수록 빠르게 커지는 특징이 있습니다.
원시 삼쌍만 골라내고 싶다면, 결국은 유클리드 공식과 동일하게 서로소/짝홀 조건이 관건이 됩니다.
“중복 없이” 삼쌍을 모으는 감각
피타고라스의 수는 정말 끝이 없습니다. 다만 블로그에서 정리할 때 독자가 헷갈리는 지점이 보통 두 가지로 모입니다.
(1) 같은 삼쌍이 여러 번 등장하거나, (2) 원시/배수가 섞여서 비교가 어려운 경우입니다. 그래서 아래 표처럼 “원시 삼쌍”과 “대표 배수”를 나눠 보면 체감이 확 좋아집니다.
원시 삼쌍과 대표 배수 비교
| 원시 삼쌍 | 생성 예(m,n) | 대표 배수 | 비고 |
| (3, 4, 5) | (m,n) = (2,1) | (6, 8, 10), (9, 12, 15) | 가장 기본 |
| (5, 12, 13) | (m,n) = (3,2) | (10, 24, 26) | 둘레/면적 예제로 자주 등장 |
| (8, 15, 17) | (m,n) = (4,1) | (16, 30, 34) | 확장하기 쉬움 |
| (7, 24, 25) | (m,n) = (4,3) | (14, 48, 50) | 24가 눈에 잘 들어오는 조합 |
계산할 때 실수 많이 나오는 부분
- m과 n을 둘 다 홀수로 잡아놓고 “왜 전부 짝수로만 나오지?” 하는 경우가 많습니다.
- 서로소 조건을 안 걸면 원시 삼쌍이 아니라 배수가 먼저 튀어나와서 목록이 지저분해집니다.
- (a, b, c)에서 a와 b는 자리 바뀌어도 같은 삼쌍이라, 정리할 땐 보통 a < b로 고정해두면 보기 편합니다.
원문에서 정리한 재표현 공식도 결국 같은 계열이라, 정리하는 목적이 “빨리 뽑아내기”인지 “원시만 모으기”인지에 따라 조건을 어디에 두느냐가 완성도를 갈라줍니다.
연습용 자료
예제 숫자를 더 보고 싶다면 아래 자료도 같이 두면 좋습니다.
유클리드 공식은 여전히 가장 표준이고, 원문에서 정리한 식은 그 공식을 “쓰기 편한 형태”로 바꾼 버전이라 보면 정확합니다.
손에 맞는 쪽을 골라서 직접 여러 조합을 만들어보면, 피타고라스의 수가 왜 이렇게 다양한 문제에 계속 등장하는지도 금방 감이 옵니다.
FAQ
Q. 피타고라스의 수는 왜 “무한히” 존재하나요?
A. 유클리드 공식에서 정수 m, n을 계속 늘릴 수 있어서 (a, b, c)가 끝없이 생성됩니다. 같은 삼쌍이 반복되는 건 조건(서로소/짝홀)을 안 걸었기 때문인 경우가 많습니다.
Q. (6, 8, 10)도 피타고라스의 수인데 왜 따로 구분하나요?
A. 성질 자체는 맞지만 (3, 4, 5)의 배수라서 “새로운 조합”이라기보다 확장판에 가깝습니다. 정리나 검색 기준을 세울 때 원시/배수를 나누면 훨씬 깔끔해집니다.
Q. 원시 삼쌍만 빠르게 골라내는 조건은 뭐가 제일 중요해요?
A. 서로소(gcd=1)와 짝홀(하나는 짝수, 하나는 홀수) 두 가지가 핵심입니다. 이걸 걸면 중복이 확 줄어듭니다.
Q. 원문에서 “새로운 공식”이라고 한 식은 완전히 다른 건가요?
A. 유클리드 공식을 m = n + k 형태로 놓고 정리한 결과라서, 근본은 같습니다. 다만 계산할 때 “차이”를 먼저 잡고 전개하는 방식이라 손에 더 잘 맞는 경우가 있습니다.
Q. 피타고라스의 수는 실제로 어디에 많이 쓰이나요?
A. 좌표 거리(2D/3D), 직교 좌표의 길이 계산, 픽셀/해상도 비율, 도면/건축에서 직각 검증 같은 곳에서 자주 등장합니다. 수학 예제에서만 끝나는 개념이 아니라 실무에서도 꽤 자주 만나게 됩니다.
'3D 2D 디자인 > 기계설계 품질' 카테고리의 다른 글
| 솔리드웍스 2025버전 도면템플릿과 시트양식 설정 완전정리 (0) | 2026.01.21 |
|---|---|
| PPAP Level 1~5 적용 시점과 제출자료: 신규 개발/변경 업무에 바로 쓰는 정리 (0) | 2025.12.23 |
| SCM440 vs AISI 303F 차이점과 용도 비교 (0) | 2025.12.14 |



